Als Fassregel von Kepler wird oft die Integrationsregel bezeichnet, die wir heute als Simpsonregel kennen, und die das Integral einer Funktion approximiert. Kepler hat die Regel auch gekannt. Aber er interessierte sich für das Volumen von Fässern.
Zunächst benötigen wir aber die Simpsonregel.
![]()
Wir implementieren Sie in Maxima.
>function intsimps (a,b) &&= (f(b)+f(a)+4*f((a+b)/2))*(b-a)/6
b + a
(b - a) (4 f(-----) + f(b) + f(a))
2
----------------------------------
6
Die Simpsonregel ist so gemacht, dass sie ein beliebiges Interpolationspolynom zweiten Grades exakt integriert. Dies führt dazu, dass tatsächlich alle Polynome dritten Grades exakt integriert werden.
Wir leiten das nicht her, sondern rechnen einfach den allgemeinen Fall nach.
>function f(x) &= a0+a1*x+a2*x^2+a3*x^3
3 2
a3 x + a2 x + a1 x + a0
Der Fehler ist in der Tat 0, wie man in der folgenden Rechnung sieht.
>&ratsimp(intsimps(a,b)), &ratsimp(%-integrate(f(x),x,a,b))
4 3 2 4 3
(3 a3 b + 4 a2 b + 6 a1 b + 12 a0 b - 3 a a3 - 4 a a2
2
- 6 a a1 - 12 a a0)/12
0
Polynome vierten Grades werden nicht mehr exakt integriert.
>function f(x) &= x^4;
Das folgende Ergebnis müsste 1/5 sein.
>&intsimps(0,1)
5
--
24
Fässer sind dreidimensionale Körper. Nach Fubini lässt sich ihr Volumen durch
![]()
berechnen, wobei F(h) die Fläche in der Höhe h ist.
Das folgende Fass ist unter der (unrealistischen) Annahme gezeichnet worden, dass der Längsschnitt eines Fasses durch eine Parabel begrenzt ist.
>plot3d("1-0.2*x^2",-1,1,rotate=1,hue=true,angle=140°):
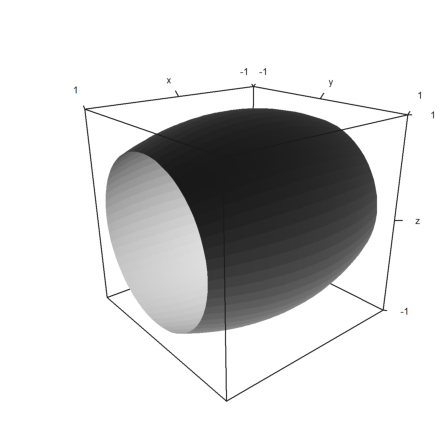
Die Begrenzung des Längsschnittes ist folgende Funktion.
>function f(x) &= 1-x^2*1/5
2
x
1 - --
5
Hier ist der Längsschnitt.
>plot2d("f(x)",r=1); plot2d("-f(x)",add=true):
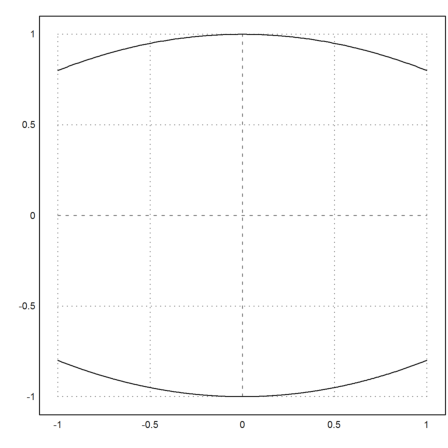
Das exakte Volumen für solch einen Drehkörper ist mit Hilfe eines Spezialfalles des Satzes von Fubini folgendermaßen zu berechnen.
![]()
In unserem, konkreten Fall bedeutet das folgendes Ergebnis.
>&integrate(pi*f(t)^2,t,-1,1), %()
656 pi
------
375
5.49569274868
Es liegt nun nahe, Keplers Fassregel für das Integral zu verwenden. Da sich der Umfang leicht messen lässt, stellen wir eine Formel für die Fläche F bei gegebenem Umfang auf.
>function F(u) &= pi*(u/(2*pi))^2
2
u
----
4 pi
Für ein Fass mit der Höhe h und dem großen Umfang U in der Mitte und dem kleinen Umfang u oben und unten (die wir als gleich annehmen) erhalten wir daher folgende Formel.
>function kepl (h,U,u) &= ratsimp(h/6*(2*F(u)+4*F(U)))
2 2
2 h U + h u
-------------
12 pi
Das ist Keplers Fassformel.
Wir testen die Formel an unserem Beispiel, von dem wir das Volumen exakt kennen.
>kepl(2,2pi,2pi*0.8), integrate("pi*(1-0.2*x^2)^2",-1,1)
5.52920307032 5.49569274868
Wir erhalten eine mäßig gute Approximation.
Es ergibt sich durch einen Zufall, dass die Formel für die Kugel exakt ist. Denn die Kugel ist die Drehfigur, die durch das Drehen der Funktion
![]()
entsteht.
>plot3d("sqrt(1-x^2)",-1,1,rotate=1,hue=true,angle=140°):
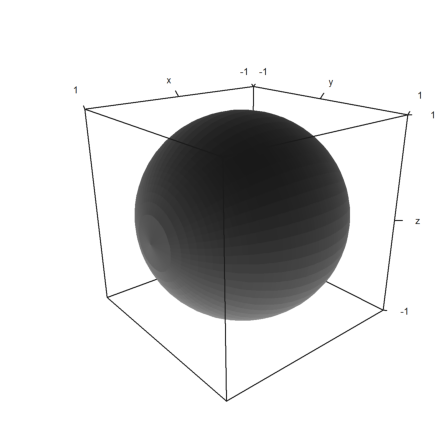
Da f(x)^2 ein quadratisches Polynom ist, liefert die Keplersche Fassregel das exakte Ergebnis.
>kepl(2,2pi,0), 4/3*pi
4.18879020479 4.18879020479
Das gleiche gilt für Kegelstümpfe, die durch lineare Funktionen begrenzt sind, wenn man die Fassregel so modifiziert, dass sie unten und oben zwei verschiedene Umfänge zulässt.
>function keplm (h,U,u1,u2) &= ratsimp(h/6*(F(u1)+4*F(U)+F(u2)))
2 2 2
4 h U + h u2 + h u1
----------------------
24 pi
Für einen Kegel sind die Umfänge 0, pi, 2pi, wenn der Radius unten gleich 1 ist. Wir erhalten in der Tat die Formel für das Volumen eines Kegels.
>&keplm(h,2*pi/2,0,2*pi)
pi h
----
3
Die Keplersche Formel stimmt nicht mehr, wenn der Längsschnitt durch Kreissektoren begrenzt wird.
Wir bestimmen ein solches Fass, dass die gleichen Umfänge hat wie das Fass, dass wir oben untersucht haben. Dessen Radien waren 0.8 oben und unten, und 1 in der Mitte.
Die Gleichung eines zur x-Achse symmetrischen Kreises, der durch (0,1) geht, ist allgemein
![]()
Wir bestimmen a so, dass er auch durch (1,0.8) geht.
>&solve(1+(4/5-a)^2=(1-a)^2,a)
8
[a = - -]
5
Damit können wir eine Funktion aufstellen, deren Graph dieser Kreis ist.
>&solve(x^2+(y-a)^2=(1-a)^2,y) with a=-8/5, function f(x) &= y with %[2]
169 2 8 169 2 8
[y = - sqrt(--- - x ) - -, y = sqrt(--- - x ) - -]
25 5 25 5
169 2 8
sqrt(--- - x ) - -
25 5
>plot2d("f(x)",r=1); plot2d("-f(x)",add=true):
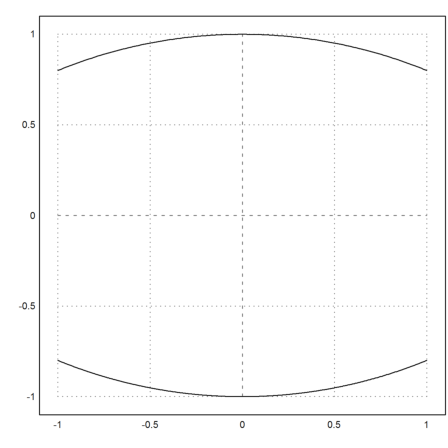
Ein solches Fass sieht optisch nicht sehr verschieden von unserem Parabelfass aus.
>plot3d("f",-1,1,rotate=1,hue=true,angle=140°):
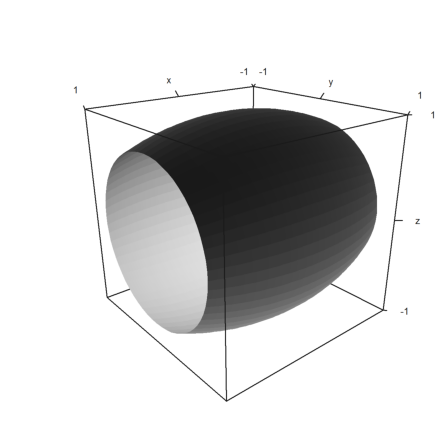
Die Approximation der Keplerschen Fassregel ist aber recht gut. Bei einem 500l-Faß wird man nur um 2 Liter betrogen.
>kepl(2,2pi,2pi*0.8), integrate("pi*f(x)^2",-1,1)
5.52920307032 5.50787741156